『エレガントな問題解決』代数編

『エレガントな問題解決』にはたくさんの演習問題が記載されています。
せっかく買ったことだし、演習問題を解いていこう。
これからやる人たちに参考になると思って、自分なりの解答を載せていきます。

自分の解答が合ってるのかがすごく心配です。（間違ったものってネットに載せていいのかな・・・と思ったり）

誤解答や説明不足、どんどんつっこんでくれるとありがたいです。
このブログは、そういう場にしたいと思っています。
（ちなみに、ぼくは、証明が説明不足であるとよく言われます。）





代数からやっていきます。（この本の中だと一番好きな分野）

演習問題

5.1.1 A, B でそれぞれの偶数および奇数を表すものとする (a) AからBへの全単射があるか (b) ZからAへの全単射があるか

この問題自体はすごく有名。(プログラミングのHelloWorldぐらいかな)
全射、単射の定義を確認する問題です。

考え方：
定義は以下の通りなんだけど、そんなに難しく考える必要はない。

f : A → B で考えるとする。
全射についての考え方は単純で、f の関数による値域が、B全体となっていれば、全射が成り立つ。

単射は少し複雑で、任意のxについて、f(x)となるxが１つしか存在しない、すなわち１対１の関係があれば、単射は成り立つ。

んでもって、両方成り立てば、全単射ということです。



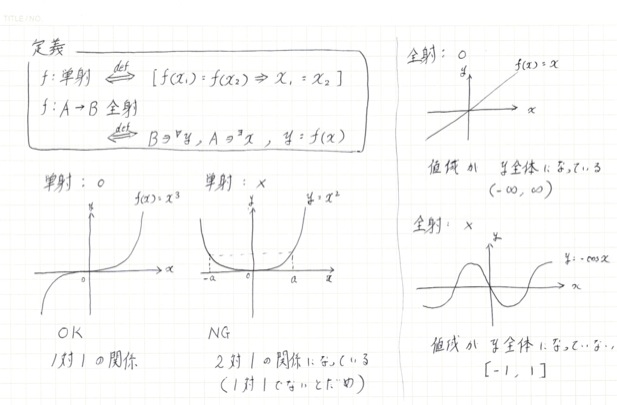
数学の公式って、限りなく抽象的だから、自分なりにかみくだくなり、具体的にしてみるなり、すると理解が早まるかも。



これから、徐々に載せていく予定です。